# Optimal Kidney Exchange

# Introduction

Over 100,000 individuals in the United States require a kidney transplant at any time, and approximately 12 people die in need of a kidney on a daily basis [1]. It is often the case that a patient requiring a kidney transplant has a relative or friend willing to donate one but cannot do so because of biological incompatibility [2]. Biological incompatibility can be due to a variety of reasons, including blood type and human leukocyte antigens (HLA). For example, donors with blood type AB can only donate to patients with blood type AB, while donors with blood type O are universal donors and can donate to patients of all blood types (O, A, B, and AB). For HLA typing, the probability of success of a transplant decreases when the donor and recipient have the same antigens [3]. Thus, biological incompatibility is a hurdle for patients who need a transplant.

To help find potential matches, kidney exchange programs have collections of these incompatible donor-patient pairs. Analyzing these pairs can help find potential exchanges between donors and patients belonging to different pairs. As shown in Figure 1 below, if we have two incompatible pairs (donor1, patient1) and (donor2, patient2) and if donor1 is compatible with patient2 and donor2 is compatible with patient1, then we can arrange donor1 to donate to patient2 and donor2 to donate to patient1.

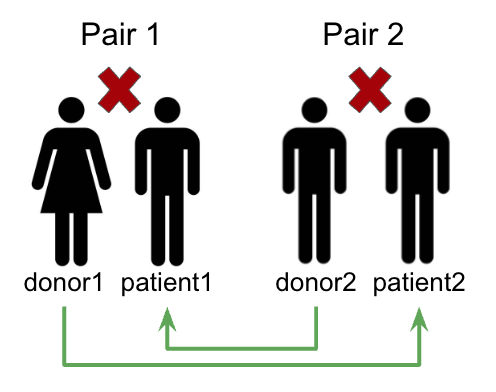
Compatibility Across Pairs

Finding these exchanges manually is extremely time-consuming, especially when the number of incompatible pairs is large. Instead, we can leverage integer optimization methods to solve this problem and maximize the number of transplants, thereby increasing survival rates. In the following sections of the report, we discuss our data, methods, and key findings. We build up our optimization model from a base model to a more complex and realistic one, which accounts for altruistic donors, match scoring, transportation costs, and surgery capacity.

Full Report Link (opens new window)

# OPTN/SRTR-based Synthetic Dataset

We utilize a synthetic kidney exchange dataset from PrefLib Kidney Data (opens new window) that mirrors real-world data characteristics based on OPTN (Organ Procurement and Transplantation Network) and SRTR (Scientific Registry of Transplant Recipients). Each pair in the dataset includes the following information:

• Patient and donor blood types (A, B, AB, O)
• Panel Reactive Antibody (PRA) level of the patient
• Number of compatible recipients for each donor
• Spousal relationship indicator
• Altruistic donor status

The dataset was generated using the methodology described in Saidman et al. (2006) [1], ensuring a realistic representation of the key aspects like blood type distributions, PRA level variations, compatibility patterns, and relationship demographics.

# Altruistic Donor {#alt_section}

So far, we implemented our model based on the "individual rationality constraint": a donor in pair ( i ) will donate a kidney if and only if their patient in pair ( i ) receives one. However, in a realistic situation, we can also have altruistic donors. As shown in Figure 2 below, altruistic donors are those who are not paired with any patient and will donate to any patient who is compatible with them [4].

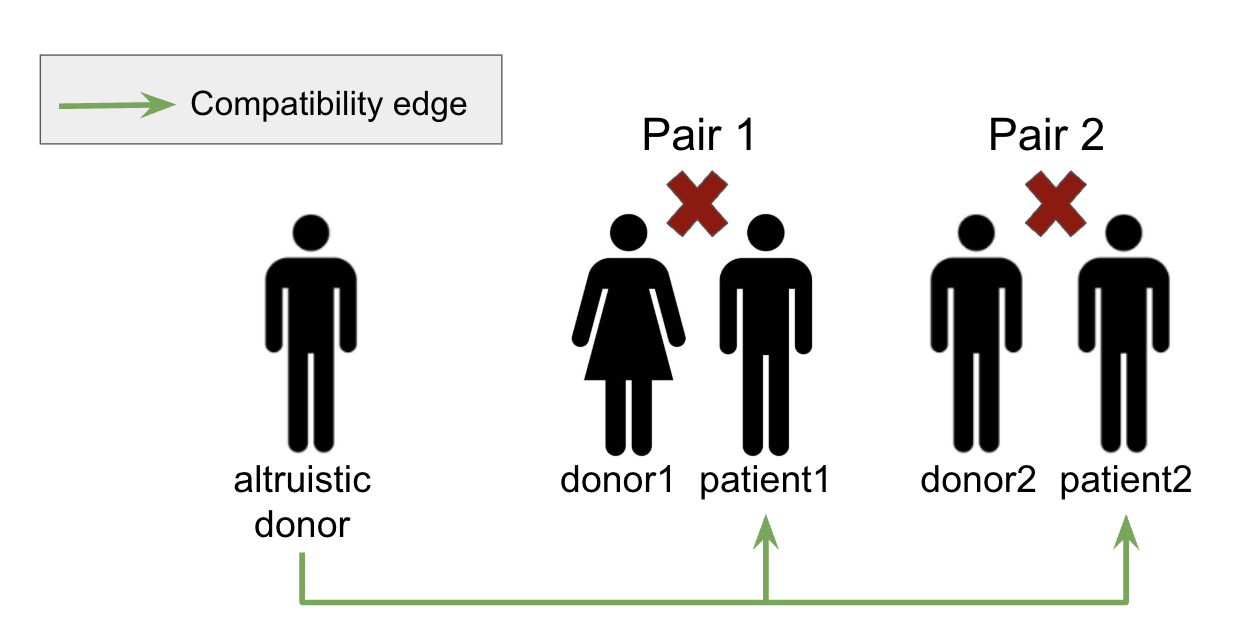
Altruistic Donor

We can incorporate altruistic donors into our model by creating another incompatible pair ( a ) with the altruistic donor and a "dummy" patient. Then, to define our compatibility matrix ( c_{ALT} ), we set ( c_{ALT}[a][j] = 1 ) if the altruistic donor is compatible with the patient in pair ( j ), but we also set ( c_{ALT}[i][a] = 1 ) for all ( i ) except ( a ) (synthetic edges) to indicate that donors in other pairs are all compatible with the "dummy" patient. This is shown in Figure 3 where, in this case, ( a = 3 ).

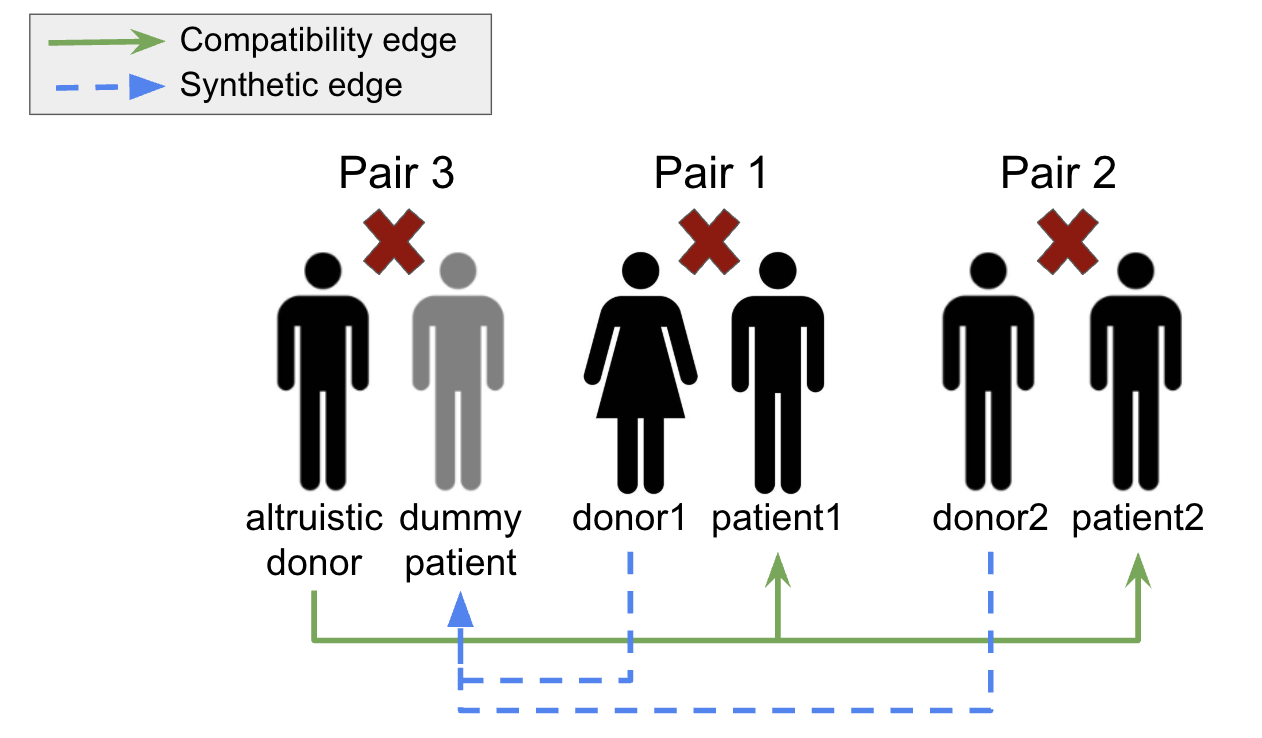
Altruistic Donor Modeling

For purposes of simplicity, we show that this model works on a smaller dataset. Let's consider the previous compatibility matrix we used in Section 3.1 in which the model achieved 0 transplants (since the patient in pair 0 did not have a donor).

To show the value of altruistic donors, let's add an altruistic donor compatible with the patient in pair 0 and the patient in pair 1 in the manner we discussed above to get the following matrix. Values are color-coded in either green or blue to indicate what type of edge they represent.

Because the altruistic donor can donate to the patient in pair 0, we expect to achieve a maximum of four transplants when running our optimization model (since the donor in pair 0 will donate to the patient in pair 1, the donor in pair 1 will donate to the patient in pair 2, the donor in pair 2 will "donate" to the "dummy" patient in pair 3, and the altruistic donor in pair 3 will donate to the patient in pair 0).

# Results

Incremental Optimization Model

Full Optimization Model

In this section, we discuss key findings and results. As we incrementally added new features to our model, we applied our model on the dataset described in Section \ref{data_section} with 1,000 donor-patient pairs and 20 transplant centers. As summarized in Figure 5 below, the model improves after incorporating each factor. In particular, our initial base model achieved an optimal solution of 640 transplants. When we incorporated altruistic donors, the number of transplants increased to 661 (an additional 21 lives saved). After incorporating match scoring, our optimal solution was 6,610, indicating that all transplants are an exact match as defined in Table \ref{tab:matching_scores}. When we subsequently minimized transportation costs through a multi-objective formulation, we improved our network, achieving the same number of transplants (661) with a transportation cost of 179,300 km. Lastly, when we accounted for surgery capacity, we achieved the same number of transplants (661) with a slightly higher transportation cost of 222,291 km (since transplant centers have finite capacity and cannot handle all the transplants that were assigned to them in the previous model formulation).

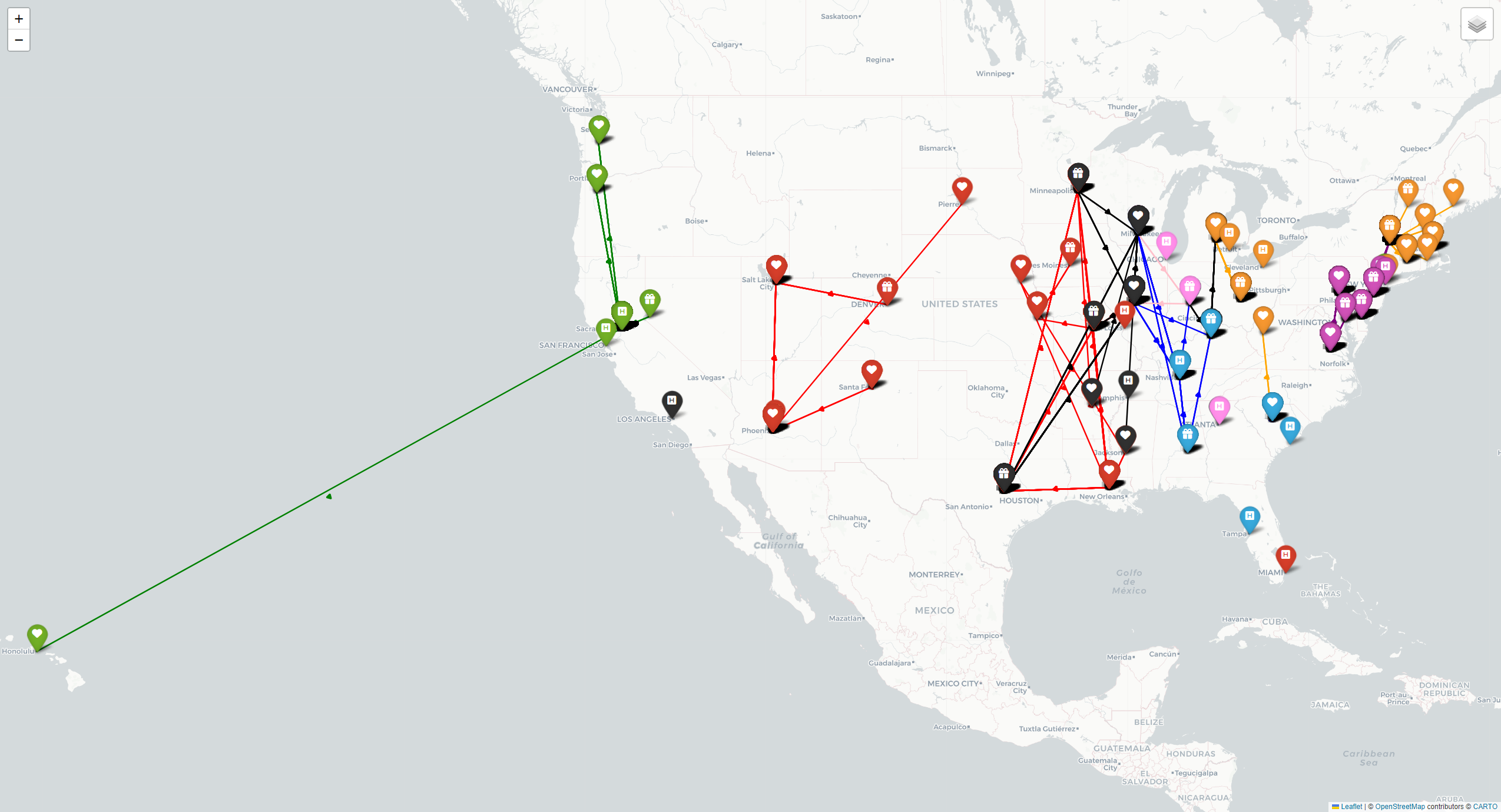
Mapping of Optimized Network

Lastly, we visualized all the matches between donors and patients that our model yielded for the large dataset of 1,000 donor-patient pairs and 20 centers in Figure 7 below. Each color represents a network of patients, donors, and transplant centers. Upon further analysis, we found that our model successfully utilized transplant centers with higher capacities, such as Massachusetts General Hospital and Mayo Clinic.